有理數 (Rational numbers)及無理數 (Irrational numbers)
有理數及無理數的定義,可看下圖

分數的有理化 (Rationalization)
分數的有理化,是指本來分母是一個含有平方根數的數值,我們要把分母化為一個有理數,做法可以用兩個例子說明
例1
例如分母是一個無理數,因為分母值不能化成一個整數。我們要先在分子及分母乘以分母的值,不但不會影響數值,而且可以使分母的平方根數值自乘後,把平方根號抵銷,使分母數值變成一個有理數。
分子是否有理數,則不在考慮之列。
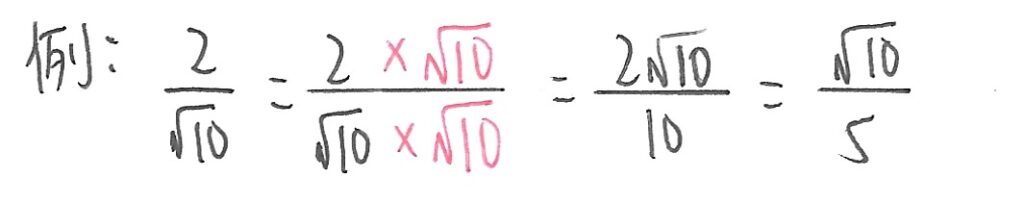
例2
如果分母是無理數的平方根,而且是兩個數相加或相減,我們可以把分母的值,在分子及分母再乘一次,但原分母是加的話,再乘一次時變減,相反亦然。
然後分子有子分乘,分母利用紅字所示的恆等式,把兩個數值也變為有理數便可。
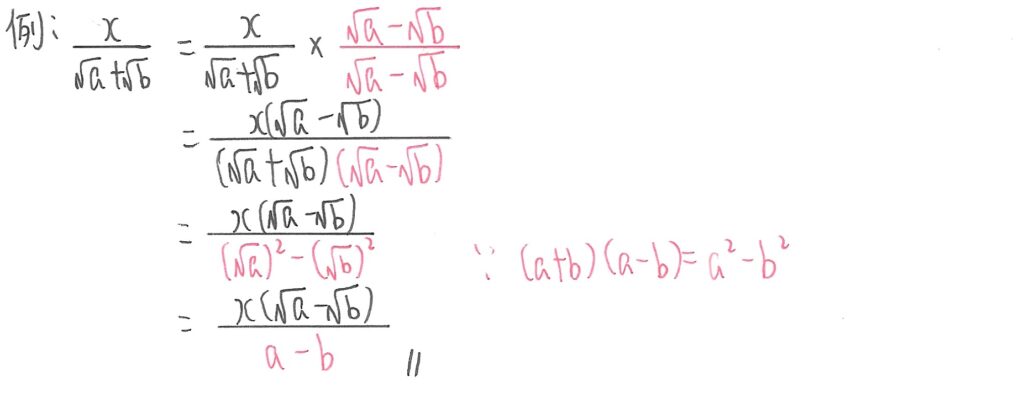
歷年試題
HKDSE中,未曾就此課題獨立出一題題目考問,但會在其他課題的題目中夾雜考問。而會考則間中會獨立考問,題目及講解可按此重溫。
