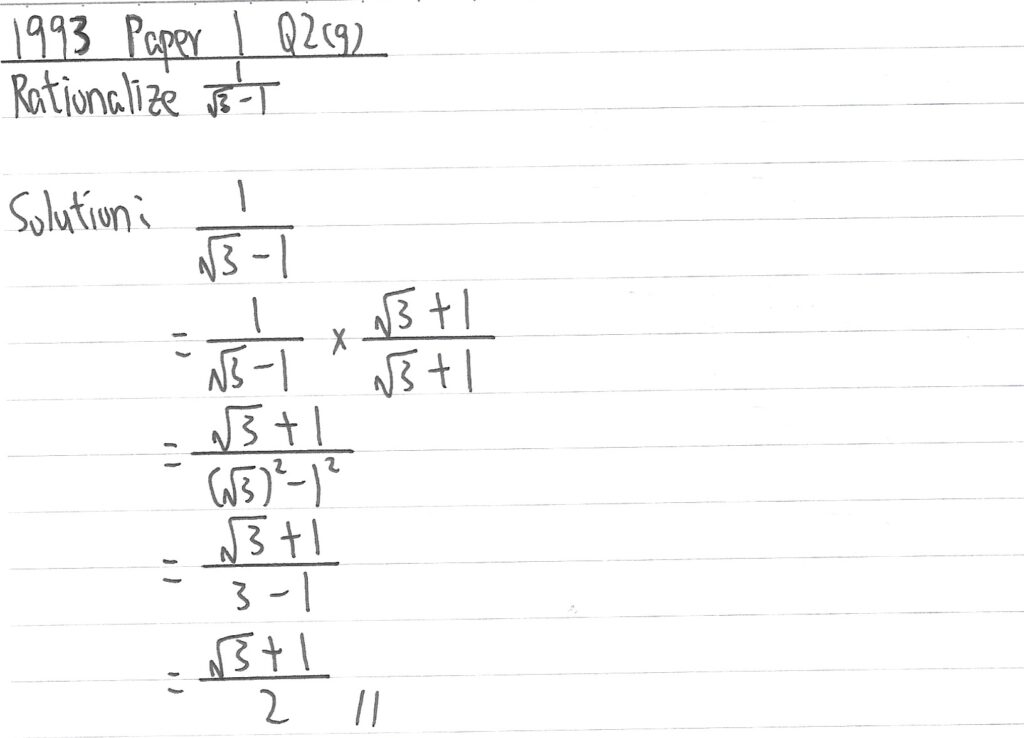以下是1993至2011年,香港中學會考(HKCEE)中,就有理化課題曾考問過的題目。
在開始講解前,請另先熟習以下課題:
平方根及根式化簡 Square Root and Surd Form
指數定律 Law of Indices
恆等式 Identities
多項式 Polynomials
2010 Paper 2 Question 39
此題考問分數除法,所以先把第二個分數的分子及分母顛倒,然後兩個分數相乘。
再利用紅字所示的指數定律化簡到只有一個a及一個b,最後把分母值,在分子分母各自乘一次便完成有理化並得出答案。

2007 Paper 2 Question 37
此題先用交叉相乘方式通分母,再用多項式的四則運算把分子及分母化簡至各自只有一個a,再把分母值,在分子分母各自乘一次便完成有理化,約簡後得出答案。

2005 Paper 2 Question 37
此題先用交叉相乘方式通分母,然後分子利用多項式運算化簡,分母利用紅字所示的恆等式計算,最後分子及分母各自乘以-1,得出正確答案。

2002 Paper 2 Question 39
此題先把左邊第二個括號數值左右相除,然後利用恆等式及基本方程式計出答案。

2000 Paper 2 Question 40
此題先在左邊括號內通分母,再全式乘以2後,把數值左右相除,再用恆等式做有理化計算出答案。

1997 Paper 1 Question 2
(a)部,先把兩個數值化為根式化簡式(Surd form),再用多項式中的同類項減法方式相減便可。
(b)部,則把分母在分子及分母各自乘一次,但加變減,再用恆等式運算作有理化。

1997 Paper 2 Question 29
此題兩個分數各自在分子及分母乘以分母值,但減變加,之後利用恆等式做有理化及後續運算得出答案。

1996 Paper 2 Question 39
左邊括號內的數值,先做通分母後兩邊乘以6,再把原分子值兩邊相除,最後用恆等式作有理化並約簡得出答案。
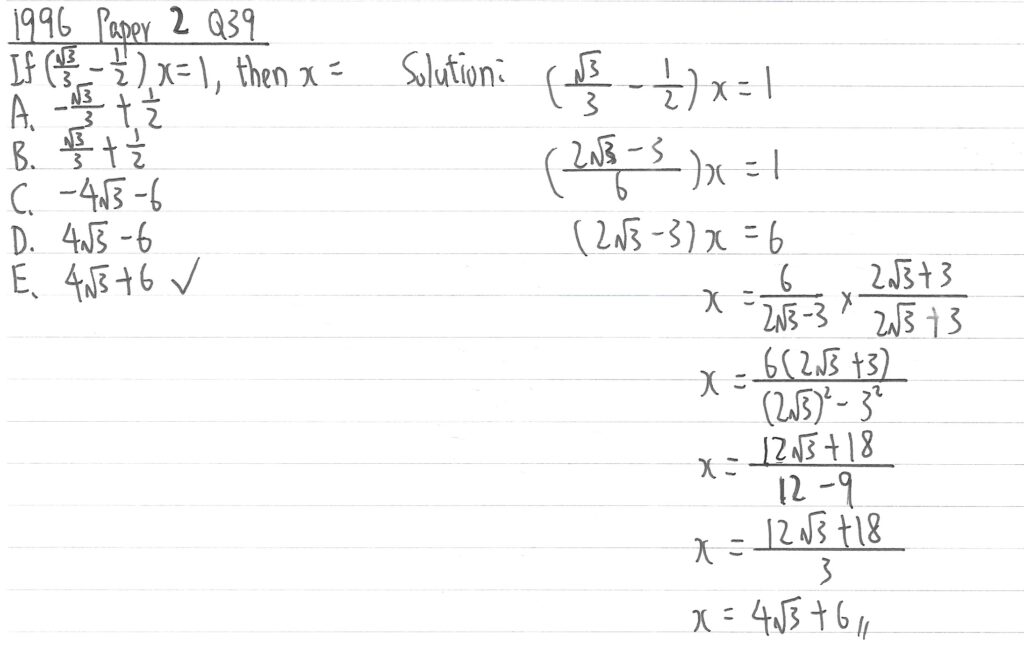
1995 Paper 2 Question 5
此題其實分母只是加減分別,所以做交叉相乘後,分母用恆等式做有理化,再約簡分數得出答案。

1994 Paper 2 Question 4
此題把a的值放到公式作運算後,利用恆等式方法作有理化並作後續計算。

1993 Paper 1 Question 2(g)
此題分數各自在分子及分母乘以分母值,但減變加,之後利用恆等式做有理化及後續運算得出答案。