在解答以下題目前,請先熟讀以下課題:
二次方程 (Quadratic Equation)
因式分解 (Factorization)
恆等式 (Identities)
2025 Paper 2 Question 5
另一種計法,是把右邊先分解為(k+1)(k-3)再把以下四個選項代左邊得出兩邊一致的結果。

2024 Paper 1 Question 3
(a)部,可以暫時不用理s值,用計算機程式計算出兩個根是7/2以及-4/3,便可以推論出來,再後每個括號的第二個數加回s便可。
(b)部,前兩項可以抽2出來,使其出現(2r-7s),後三項則可根據(a)部結果照抄,然後抽出(2r-7s)出來再做因此分解便可。
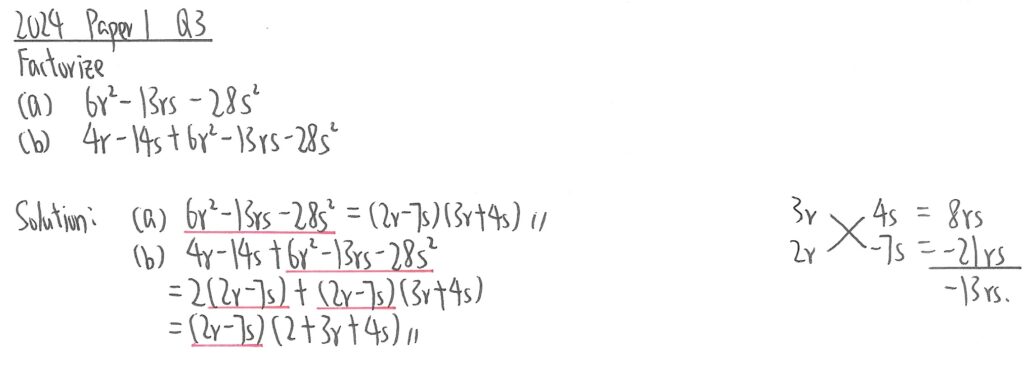
2024 Paper 2 Question 7
此題可以先把右邊的項放到左邊,再抽出(m-1)出來便可做因式分解。

2023 Paper 2 Question 4
前三項可以用十字分解法做因此分解,後兩項先把4抽出來,然後兩邊再抽(x+y)便可得出答案。
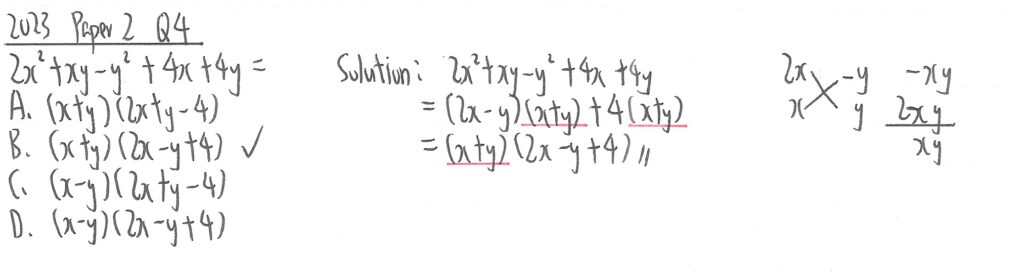
2022 Paper 2 Question 4
此題先左右分解把兩個括號相乘,再左右移項得出一組二次方程。之後大家暫時先不理會c,用計算機程式算出兩個根值分別是2及4,再把根加回c便可。
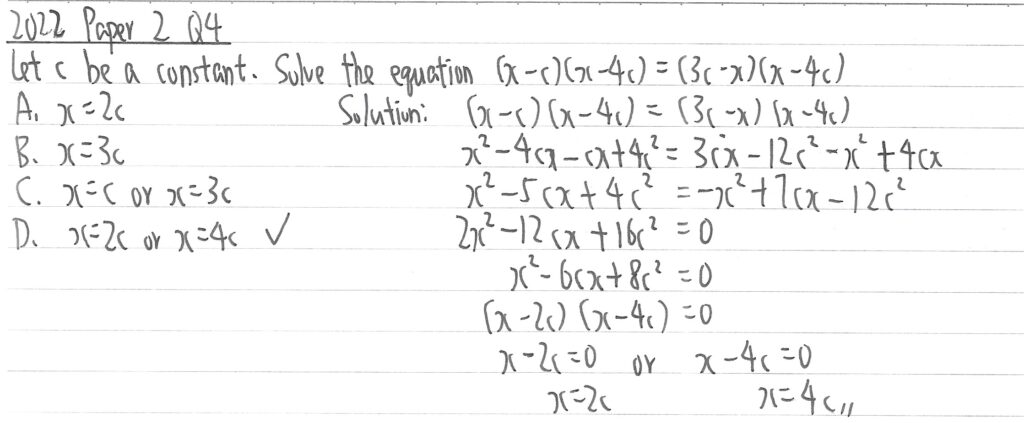
2021 Paper 1 Question 3
(a)部,大家暫時不用理會y,利用計算機程式會計出兩個根分別是1/2及-2/3,再推論出應做的因式分解。
(b)部,前兩項先把4抽出來,後三項根據(a)部結果,再抽(2x-y)便可完成因式分解。
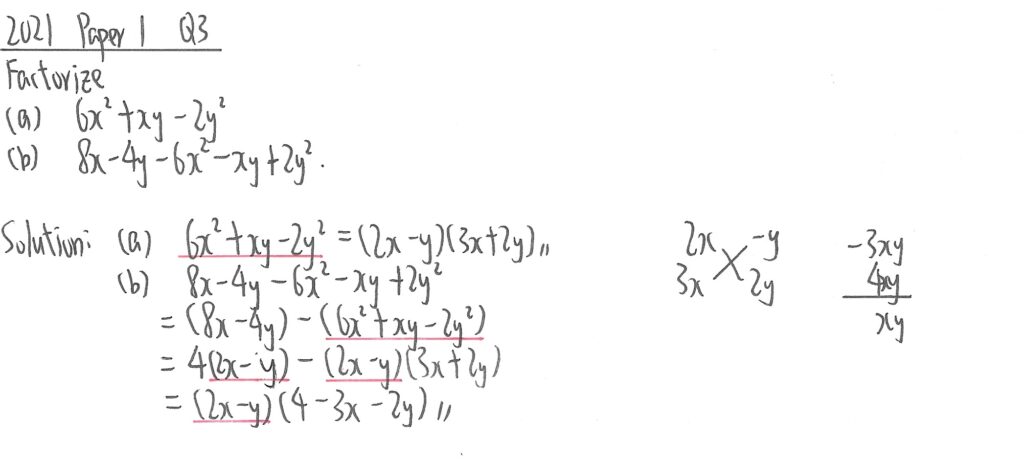
2020 Paper 1 Question 2
(a)部,如果利算程式計算,會得到兩個根為2及-3,然後把其移到左邊,不想理會右邊=0便可。
(b)部,只需先抽出a2,便可套用(a)部結果得出答案。
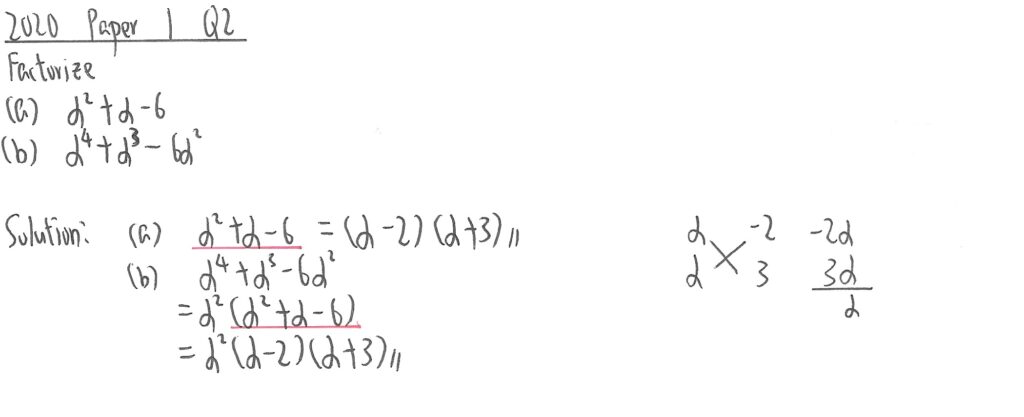
2019 Paper 1 Question 4
(a)部,使用紅字所示恆等式便可做因式分解。
(b)部,先把n出抽來,再用計算機程式計算出兩個根分別為3/2及-5後把移項到左邊便可做到因式分解。
(c)部其實是前兩部的混合體,唯後三項留意正負號便可。

2017 Paper 1 Question 3
(a)部,先暫時不理會y,再用計算機程式計算出兩個根分別為3及1後移項到左邊再加y便可做到因式分解。
(b)部首三項根據(a)部結果,後兩項則把11抽出來,再抽(x-3y)再另做因式分解。
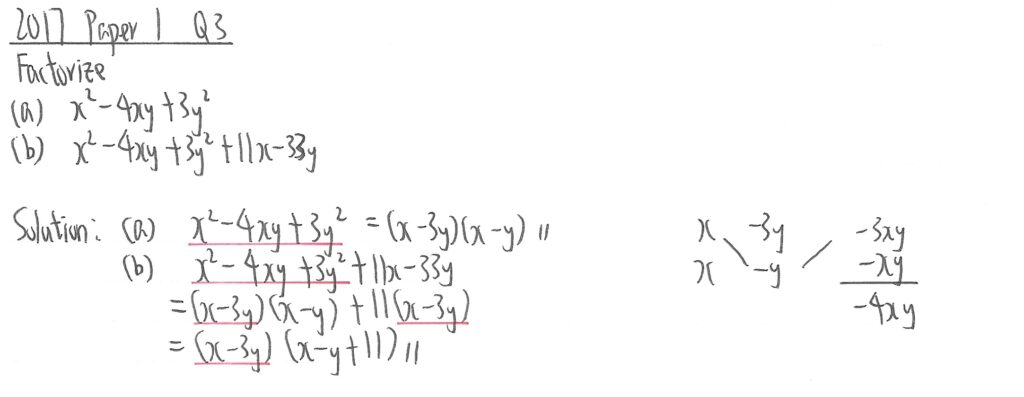
2016 Paper 1 Question 4
(a)部,只需把5抽出來做可。
(b)部,先暫時不理會n,再用計算機程式計算出兩個根分別為2及-3後把移項到左邊再加n便可做到因式分解。
(c)部其實是前兩部的混合體,唯後兩項留意正負號便可。
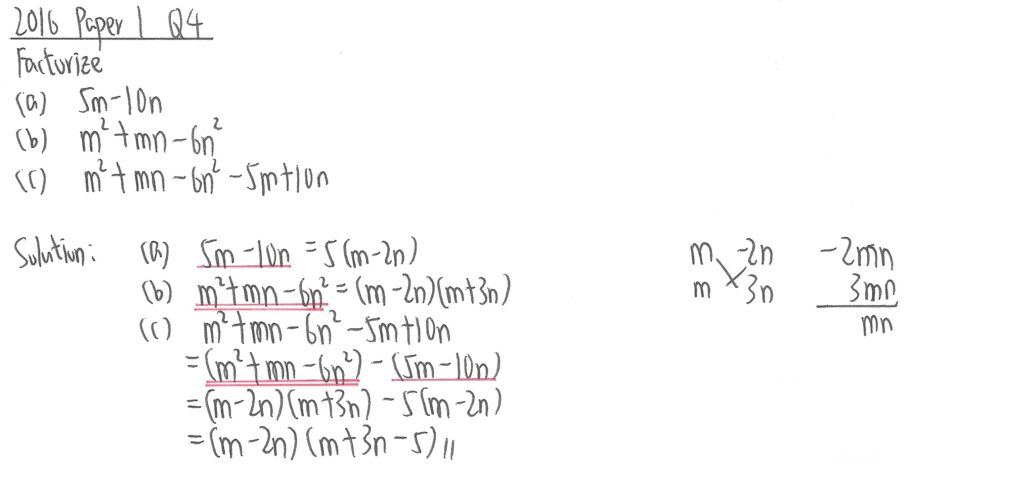
2015 Paper 2 Question 7
把問題第一組式為(1)式,第二組式為(2)式,把(2)式數值全部乘以-2,使兩組方程式首兩項的係數一致,再比較常數項的差異便可。

2014 Paper 1 Question 2
(a)部,利用計算機程式計算出兩根分別是-1及3後移項到左邊便可做到因式分解。
(b)部,首兩項抽b2,後三項利用(a)部結果便可。
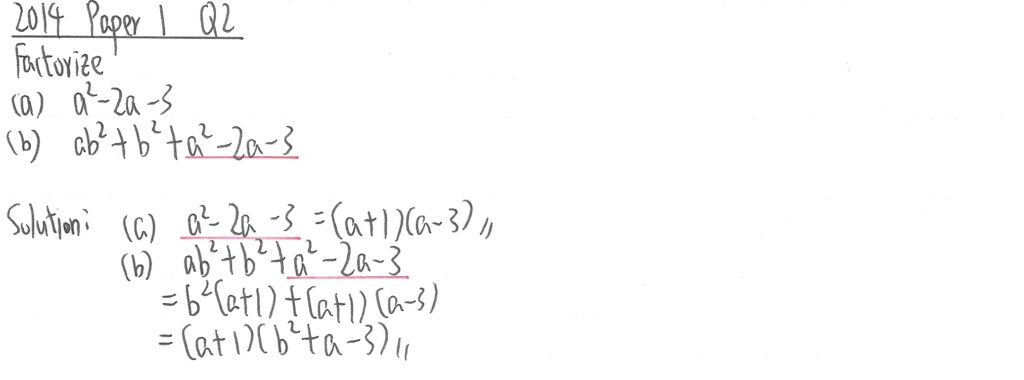
2013 Paper 2 Question 6
此題可以利用a2-b2=(a+b)(a-b)的恆等式做因式分解後找出兩個根。

