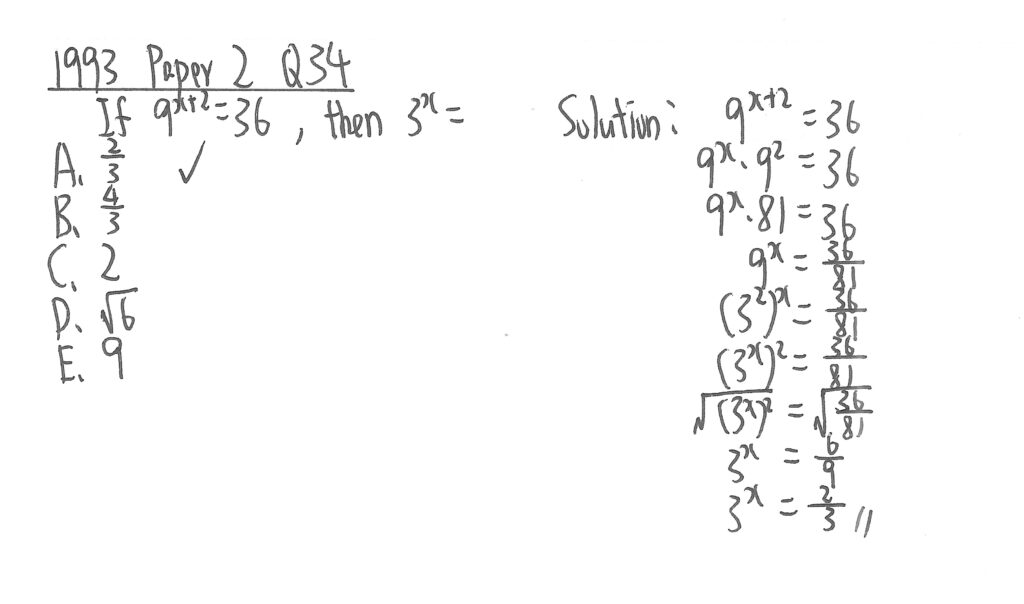此文會示範及分析1993年2011年數學科卷二,有關「指數定律」(Law of Indices)的歷年題目。
2011 Paper 2 Question 1
此題只需利用紅字所示定律,並留意在底數是負數的情況下,單數次方仍會得出負數值,便可求出答案。
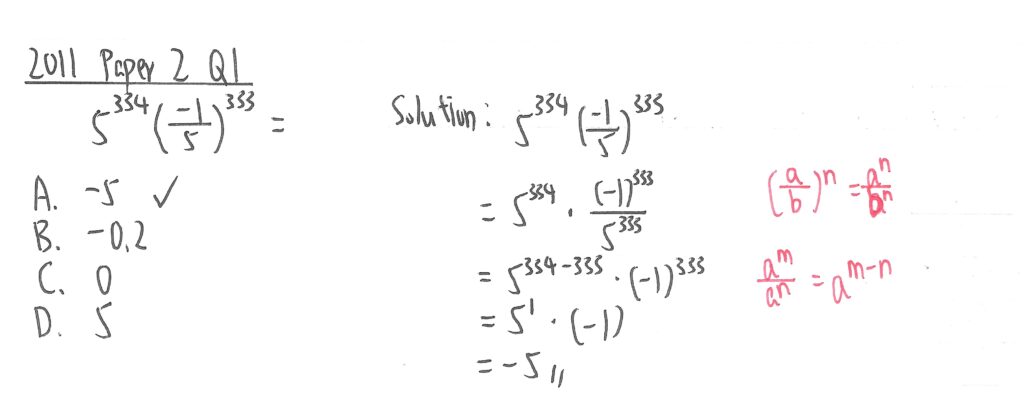
2010 Paper 2 Question 2
此題只需利用紅字所示定律便可求出答案。
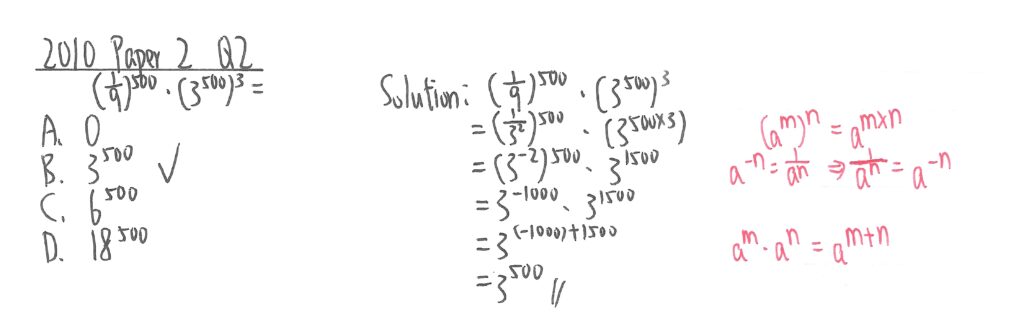
2009 Paper 2 Question 1
此題兩個數值的指數是一樣,只此只需把兩個底數相乘,次方不變便可。
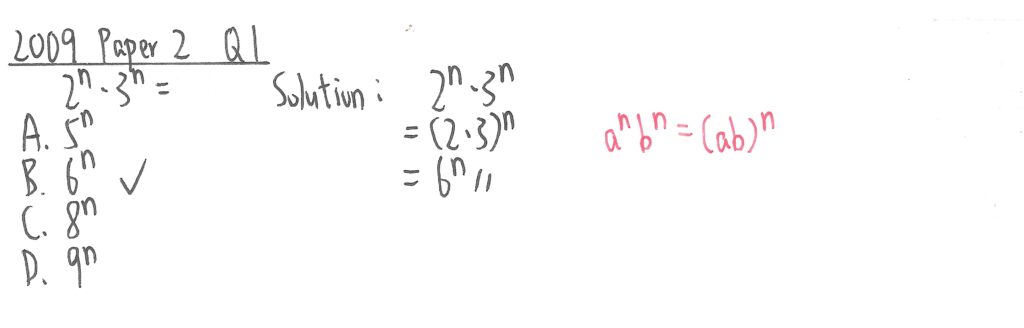
2008 Paper 2 Question 1
此題只需利用紅字所示定律,並留意在底數是負數的情況下,單數次方仍會得出負數值,便可求出答案。
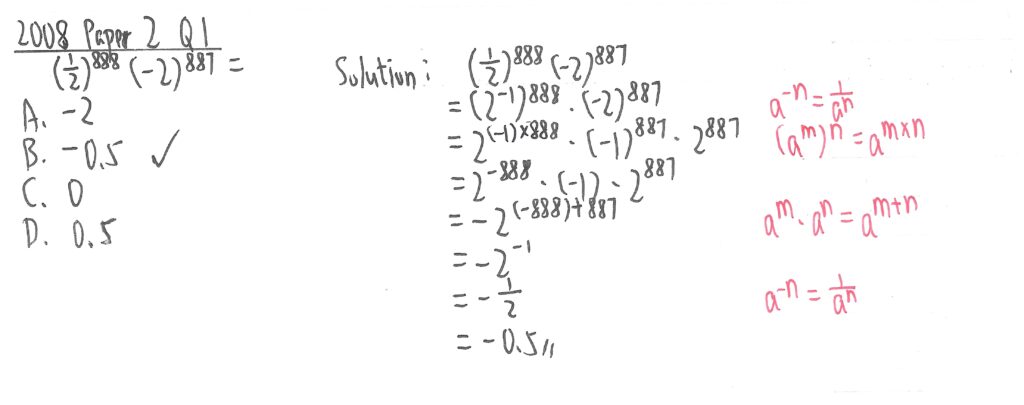
2007 Paper 2 Question 1
此題先把4化作22,再用紅字所示定律使兩個數值的指數一樣後,便可底數相乘求出答案。
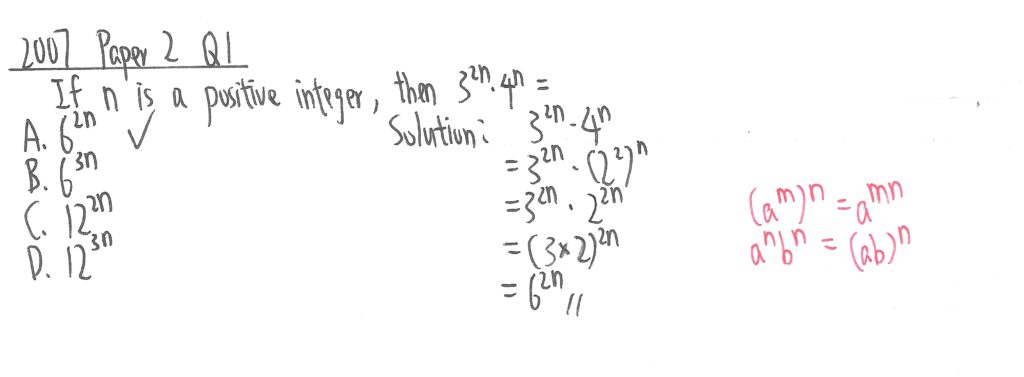
2006 Paper 2 Question 1
此題利用紅字所示定律,然後數字和X各自相乘得出答案。
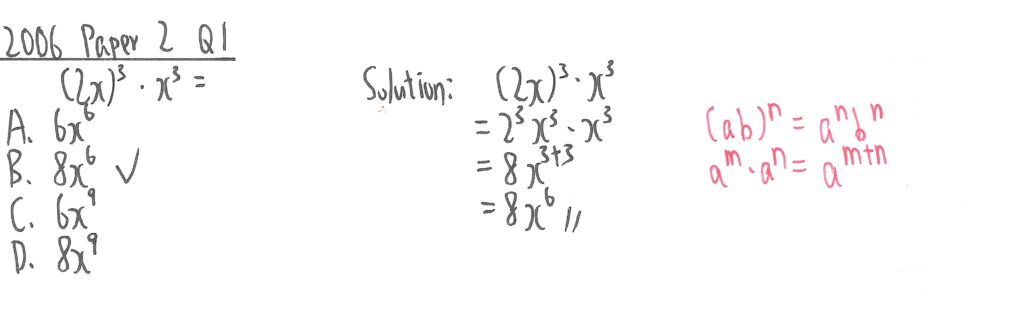
2005 Paper 2 Question 1
此題先處理括號內的加法,再利用紅字所示定律把a的次方相加,而2則保留。
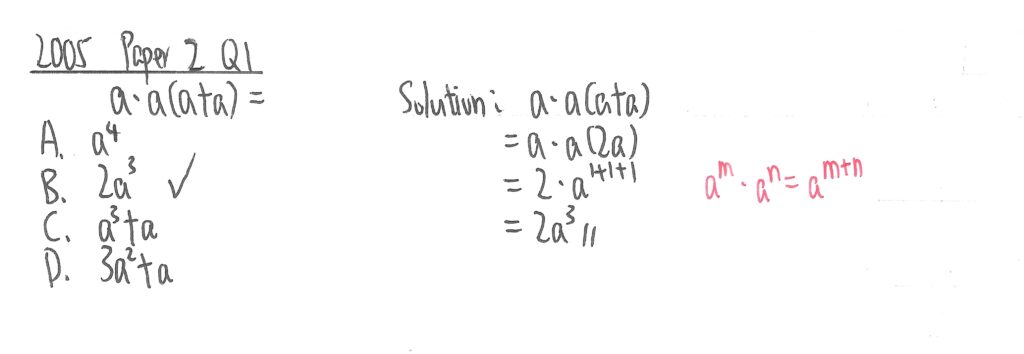
2004 Paper 2 Question 1
此題先把22n,利用(22)n的定律,使所有數值的指數同為n,最後3個底數相乘或相除便可得出答案。
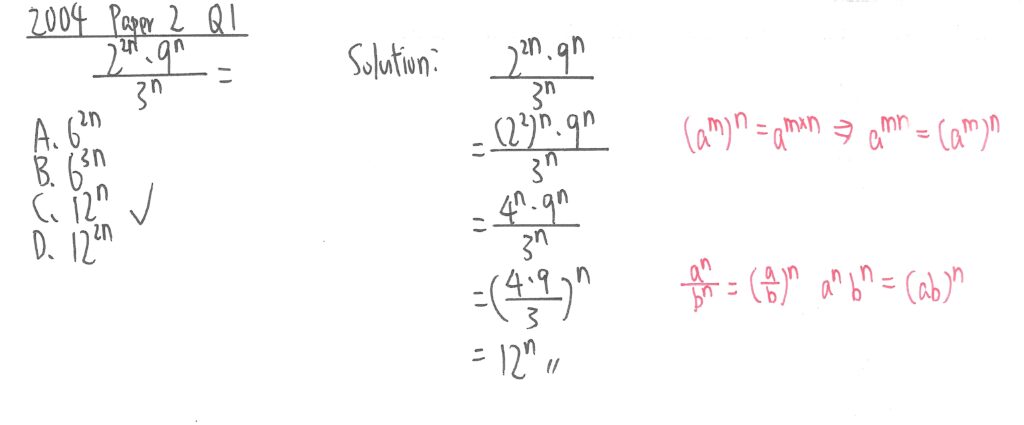
2003 Paper 2 Question 4
此題先把後半部化成底數3,然後再用紅字所示定律經計算後求出答案。
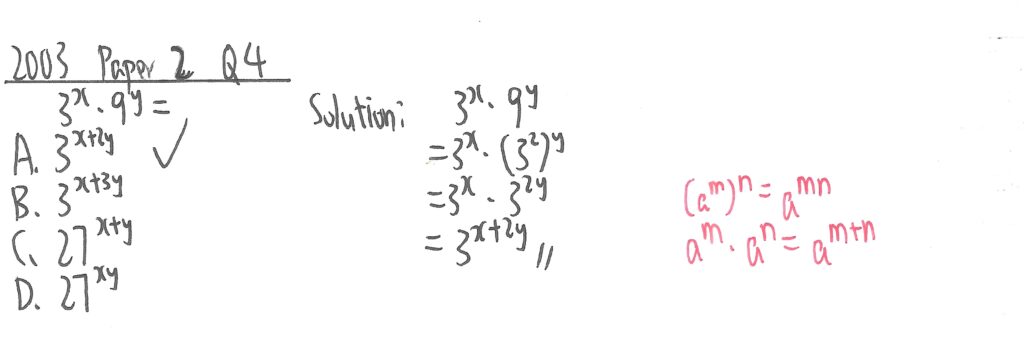
2002 Paper 2 Question 3
此題先把後半部化成底數2,然後再用紅字所示定律經計算後求出答案。
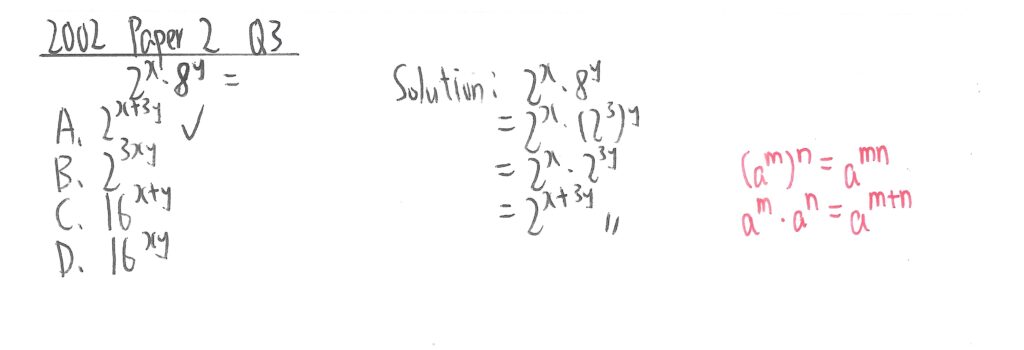
2001 Paper 2 Question 10
此題先把題目分拆成兩個分數,因為同分母的加法,相加時分母不變,可看到前半部剛好等於1,而後半部則利用「指數相減」定律便可計出答案。
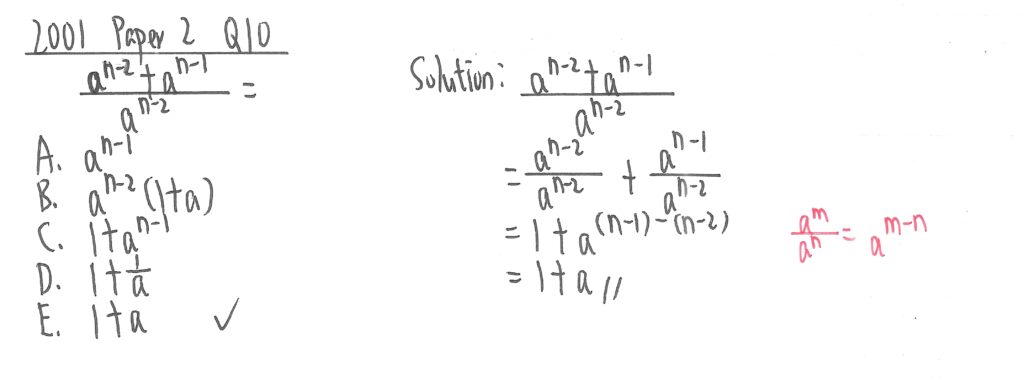
2000 Paper 2 Question 3
此題利用紅字所示定律便可求出答案。

1999 Paper 2 Question 4
此題先把16化成42,再利用紅字所示定律得出4x,把此數變成題目中的a便可求出答案。
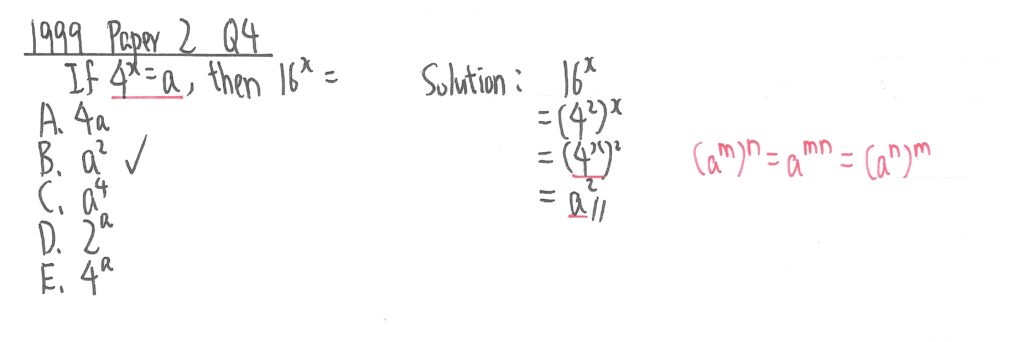
1998 Paper 2 Question 7
此題利用紅字所示定律便可求出答案。
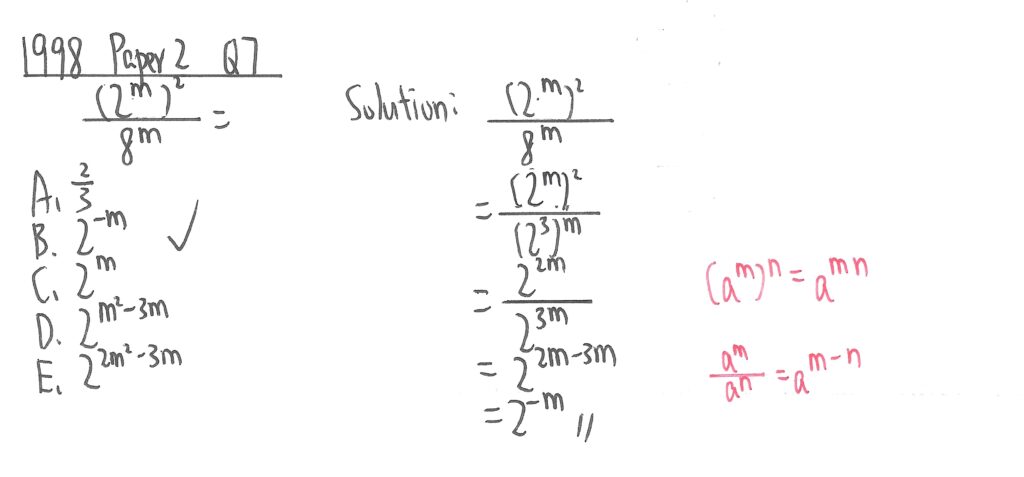
1997 Paper 2 Question 2
此題先把兩邊的底數各自化作2,再利用紅字所示定律簡化指數後,只需以方程式求出x的值便可,不用再理會底數。
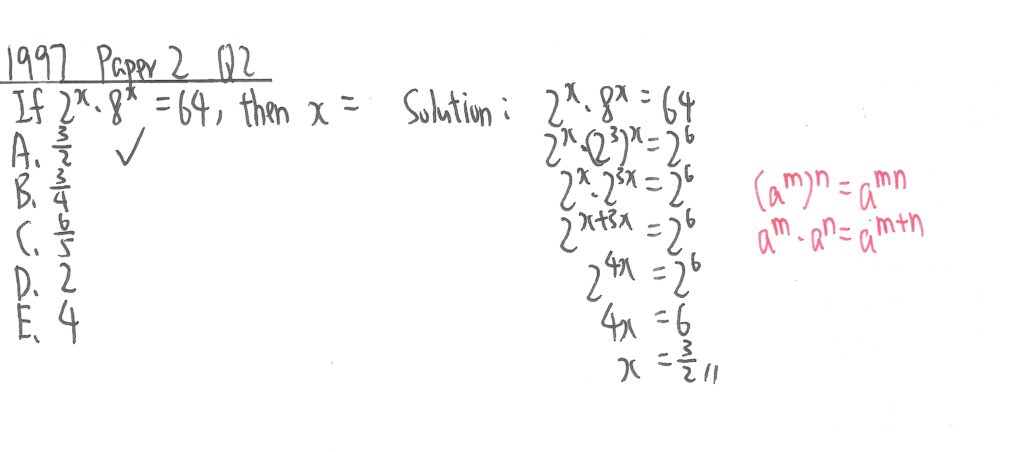
1996 Paper 2 Question 2
此題先把27化成底數3,再用紅字所示定律計算便可。
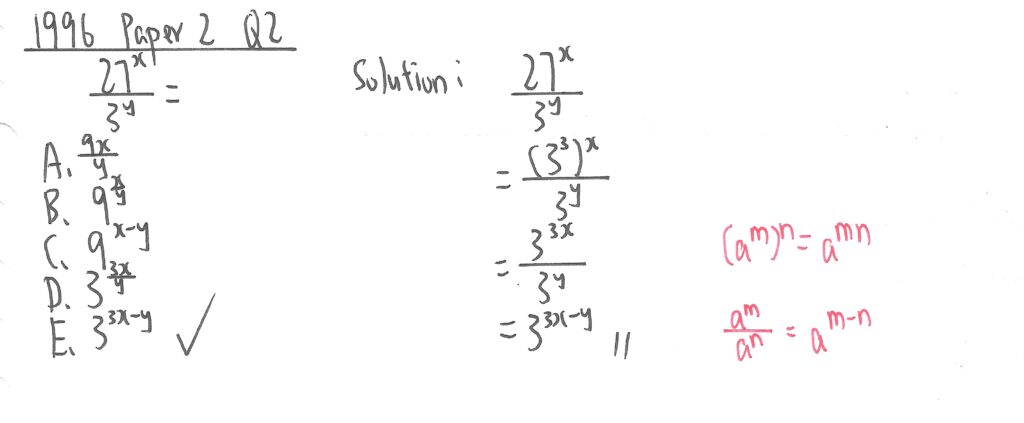
1995 Paper 2 Question 4
此題利用紅字所示定律便可求出答案。
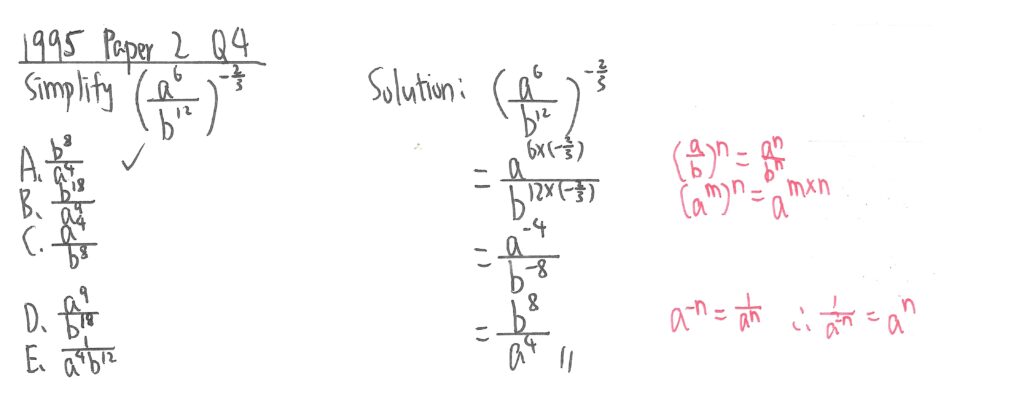
1994 Paper 2 Question 33
此題利用紅字所示定律便可求出答案。
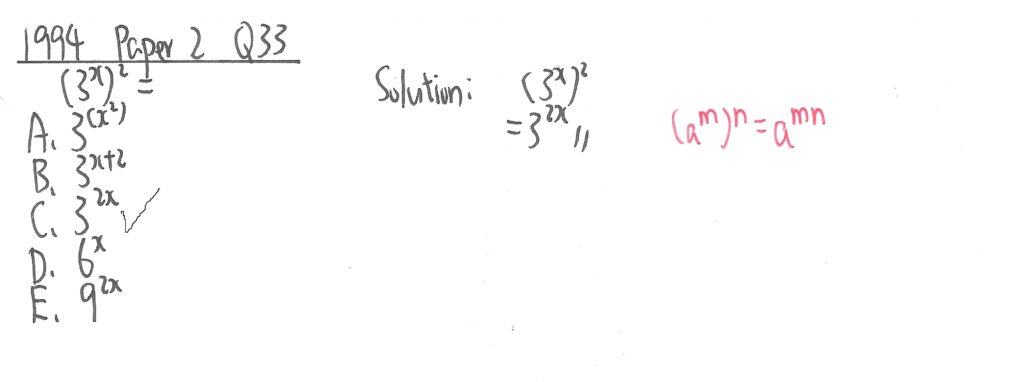
1993 Paper 2 Question 34
左邊指數相加,可以分別化作同底數相乘,最後按要求化成題目要求的答案便可。