率 (Rate)
率(Rate),是指兩個不同單位的數值相除,所以得出的答案是有兩個單位的,例如:
時薪: $50/小時 (即每小所得薪金是$50)
速率: 70km/h (即每小時行走70公里)
例如由A城到B城的總長度為180公里,一輛汽車用了3小時行畢全程,即平均時速為60公里/小時。
比 (Ratio)
比(Ratio)即是兩個相同單的數值相除,所以答案是沒有單位的。通常的表達方式是a:b,a可理解為分數中的分子,而b則為分數中的分母,例如:
1:2, 2:3, 3:2
例1

題目是要找出男生與女生的比例,即是求出「男生:女生」的比率。
在此可以先用分數形式表達,分子是男生人數,而分母則是女生人數,然後把分數約至最簡,再以A:B方式表達便可。
下圖可以表達如兩個分數數值相同,也可以說是兩者比例相同,前提是所有數目不等於0,否則會出現分母為0的不可出現情況。
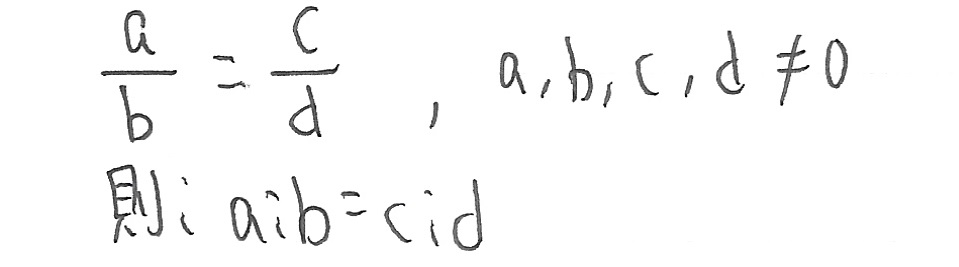
例2
當大家計算比例時,記得留意兩個數值的單位必須要是相同,例如:
一盒蘋果汁有800毫升,一盒橙汁有1.2升,求蘋果汁與橙汁的比例。
留意蘋果汁是以毫升為單位,而橙汁則以升為單位,我們要先把兩個數值比為同一單位,例如把橙汁化為毫升,即:
蘋果汁:橙汁=800毫升:1200毫升
經約簡後,最終數值就是2:3,單位也可以約走,因為兩者也是同一單位。
例3: 三項比
試題中較常出現是有兩個比例,有三個數值,其中一個在兩個比例也有,但數值不一樣,例如:

簡單而言,就是兩個比例也有b,我們可以先求兩個b的值的最小公倍數(LCM),再把同一比例的所有數值乘以相同的數值,使b可以出現同樣數值的同時,不影響個別比例的值(即是分數中的「擴分」概念)。
例4: k方法 (k method)
試題中另一較常出現的題目,就是計算出題目情境中,每個人/群體分別有多少東西可分配到/有多少人等等。

考試會要求利用k方法(k method),如上圖中,大雄、靜香和小夫可分糖果比較為3:5:2,三人分到的糖果數量應分別是3k、5k及2k粒。
題目指總共有50粒糖果,三人總共有10份糖果,所以是10k=50,故得出k是5,即每一份糖果有5粒,再按比例分配,可得出三人最終可分配到的糖果數目。
歷年試題
HKDSE由2012年開考至今,大部份年度會就此課題獨立出題,但有時會與其他課題夾雜,例如恆等式、主項轉換和指數定律。可按以下連結看試題分析:
HKCEE題目 (1993至2011年)
