聯立方程(Simultaneous)的特性,是需要解出兩個未知數的數值。我們不可能只靠一條公式,求出兩個未知的當中,各自的唯一答案(只能夠找出兩個數值中多個符合公式的答案)。因此,要解聯立方程,需要兩條式,使兩個未知數的結果,均同時能符合兩條公式的結果。由於是有兩個未知數,此也稱為「二元一次方程式 (Linear Equations in Two Unknowns)m
解題方法
在中學的數學必修課程,解答聯立方程有三個方法:
(1) 代入法 (Method of Substitution)
(2) 消除法 (Method of Elimination)
(3) 圖解法 (Graphical Method)
在公開考試中,甲部題目通常只需使用以上(1)或(2)的方法,很少要求畫圖求結果。
代入法 Method of Substitution
「代入法」即是把其中一條公式的數值,代入到另一條公式進行計算。例如,第一條公式是x=2y,而第二條公式是x+2y=4,我們可以把第一條公式代入第二條公式的x項,使公司成為2y+2y=4,從而先計出y=1。以下是兩個例子
例1
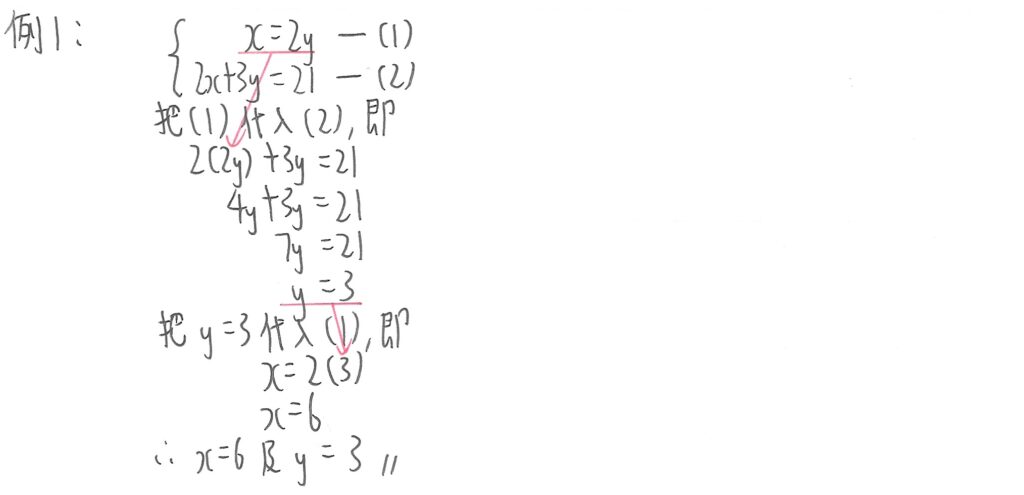
在(1)式中,已經知道x=2y,所以可以直接把此代入到(2)式中,即(2)式所有x代入2y,先計算y的值。然後把經計算出來的y值代入其中一式,計出x的值,便完成計算出兩個未知數,在兩條式均符合結果的唯一數值。
例2
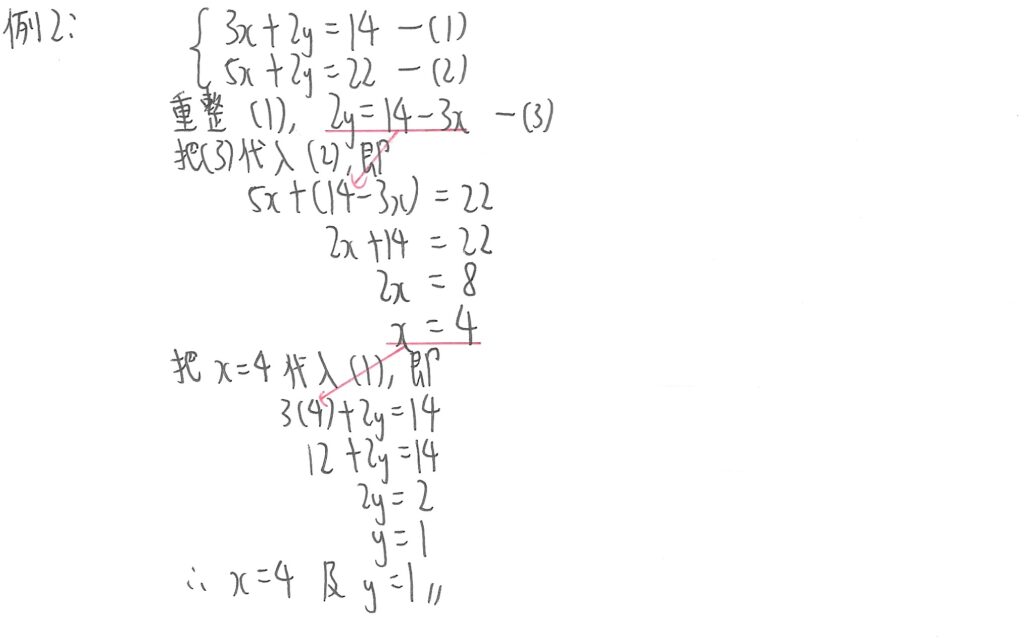
此例子的兩式中,左邊同時有x和y,而兩項的係數也是大於1。不過大家可以看到兩式中的y係數也是2,所以我們可以先在其中一式中,以主項轉換方式,以2y作為主項,然後把右邊的值代入到另一式,先計算x值,再用計算出來的x值代入到其中一條公式再計算y值便可。
以上是代入法中比較簡單的例子,更多解說可按本文最後講解公開考試題目的文章連結。
消除法 Method of Elimination
「消除法」是把兩式互相加或減,使到暫時只有一個未知數,先計算該未知數,然後把結果代入其中一式,再計算另一未知數值。
例3
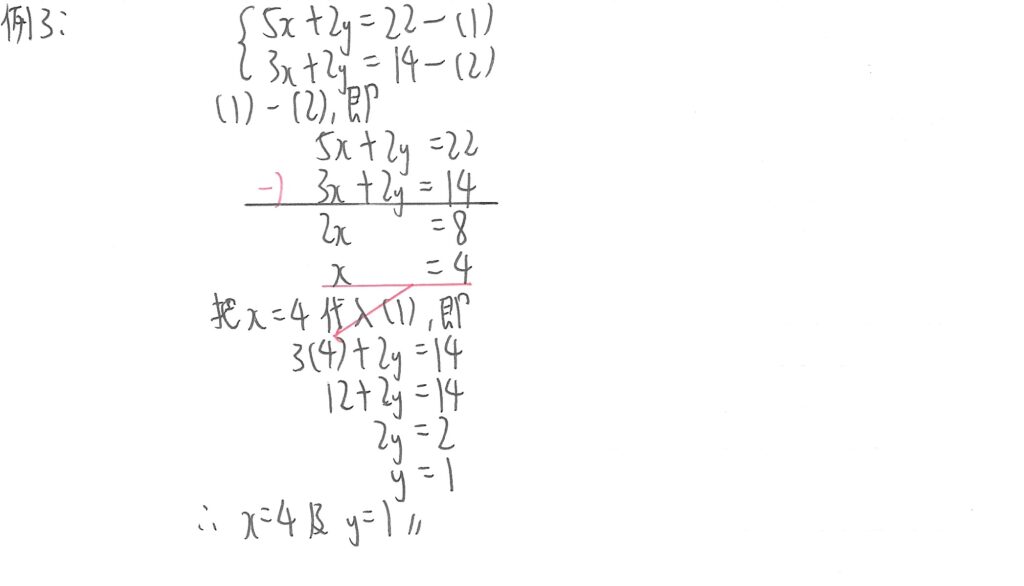
此例其實和上面例2一樣,不過我們現在先把(1)式減去(2)式,左邊同類項相減,同時右邊數值相減,使左邊暫時只有x值,先計算x的值,再把其代入其中一式,計算y的值便可。
例4

此題兩式各自的x和y項的係數不同,不過可以先把其中一式的數值倍大,使到兩式中,x或y值的係數一樣,如上圖中把(1)式係數及數值全部乘以2,使兩式同時出現2x,便可以把(1)式減去(2)式,先計算y值,再代入其中一式求x值便可。
歷年試題解說
在HKDSE中,間中會就此課題獨立出題,此課題會經常夾雜在其他課題中出現的,例如率和比 (Rate and Ratio)、變分(Variation)等等,因此此課題可能會幫助解答多於一題題目的。
HKDSE題目
HKCEE題目 (1993至2011年)
