變分(Variations)是數學教必修部份中,每年必考的課題之一。卷一大部份題目均會在甲(2)部(Section A(2))出現,並且大多會夾雜其他課題在同一題考問。而卷二也是熱門必考的獨立題目之一。
變分可以分為四種:
正變 (Direct Variation)
反變 (Inverse Variation)
聯變 (Joint Variation)
部份變 (Partial Variation)
正變 Direct Variation
正變(Direct Variation),即是一個未知數(在此稱為y),與另一個數值的變動(在此稱為x)有正變關係,簡單而言就是y隨x正變,如下面例子

理實生活例子,例如某條巴士路線每人收費$10,所有乘客均是同價。如有3人上車,總車費收入就是$30;有20人上車的話,總收入是$200。
通常我們會利用k方法(k-method)表示,上段例子我們的k就是10,因為y隨10x正變,即是當x位乘客上車,總收入是$10乘x。
大家不要以為x增加時,y值一定也會增加。這其實是不一定的,因為y可以隨-2x正變,即當x=1時,y=-1,而x=10時,y=-20。大家可以發現,x值雖然增加了,但y值反而下降。
通常在考試題目時會有以下類型,但很多時不會只是正變,而是下文會提及到的「聯變」及「部份變」。
例1

此類題目通常要求利用k方法,先找出k的值,即當x變動時,y變動的倍數。
題目前半部提供了當x=2,y=48,先設一組公式,左邊是y,右邊是含x的,右邊另加k,表示y隨含x的數值正變。
下一步,代2入x,同時代48入y,利用基本方程式求出k值是3,從而得出y=3(x+2)2。
後半部,當得到k值,並設了上段所說的公式後,便開始解答問題後半部,即代4入x,求出y值便完成。
例2

另一考問方法,此類問題通常在卷二出現。題目會說y隨x變動,當然x可以是有次方或者根號等等,之後會提供x上升或下降的百份比,要求計算y的百份比改變(上升或下降)。
在此,可以先用k方法,得出y0,表示是y的原值。之後設y1是x數值改變後的值,可以在所有未知數拼在一起,會發現未知數其實就是y0的值,所以可以化作y0。
最後一步就是利用百份比上升/下降的公式,求出y上升的百份比。
反變 Inverse Variation
反變(Inverse Variation),簡單而言就是y隨x的倒數變動,即:
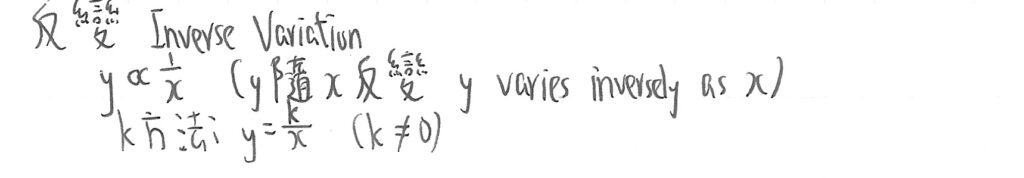
做法其實和正變分別不大,但x作為倒數,即是放在分數的分母中。
其實大家可以理解為平分東西。例如,有$1000獎金,有10名參賽者參加問答比賽,答對全部問題者可以平分獎金,下表是勝出者人數與每人可得獎金的關係:
| 勝出者人數 | 每人獎金 | |
| 1 | $1000 | $1000/1 |
| 2 | $500 | $1000/2 |
| 4 | $250 | $1000/4 |
| 5 | $200 | $1000/5 |
| 10 | $100 | $1000/10 |
可以見到,當勝出者愈多,每人平均可得獎金金額愈少,這就是「反變」的典型例子。
例3

這類例子做法和正變一樣,只是含x的部份要放在分數中的分母,先找出k值,再解答問題後半部求y值。
例4

問及y的百份比改變也是和正變同樣處理方法,不過含x部份要放在分數中的分母。
聯變 (Joint Variation)
聯變(Joint Variation),就是x會同時隨y及z正變或反變,y和z可以是同時正變、同時反變,或是其一個正變,另一個則反變。
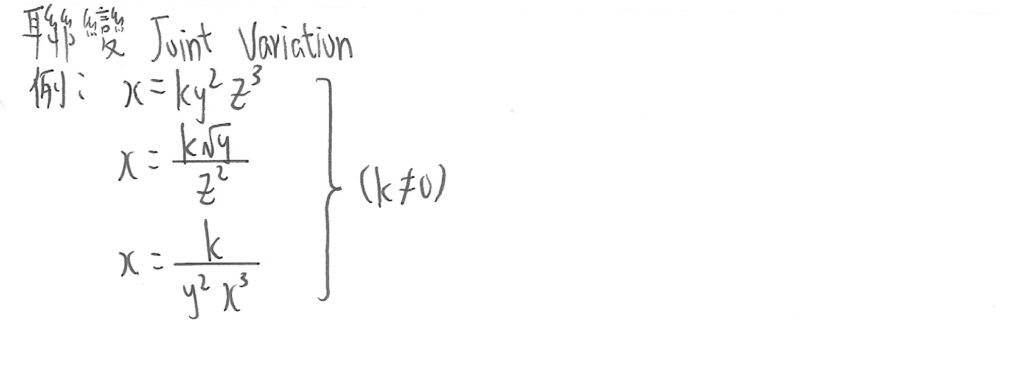
上面示範了三種當出現當x與兩個未知數有變分時的情況。考慮最多就只會問到x隨兩個未知數正變/反變。
以上計算的例子會較多出現在聯變,主要出現在卷二題目,此等題目會在考試題目講解時再作詳解。
部份變 (Partial Variation)
部份變 (Partial Variation),即是x分別隨y及z正變/反變。

題目會出現「部份」(partly)字眼,暗示這是部份變,會有兩個組未知數相加的。所以k方法時要設兩個k,分別是k1及k2。近年卷一題目如出現在甲(2)部(Section A(2)),甚或是乙部(Section B)出現時,都會是部份變題目。
另外,題目可能會出現「一部份為常數」(Partly constant),另一部份隨x2正變,那麼我們k1不會再跟任何未知數相乘,而k2則與x2相乘。
由於有兩個k值,所以題目會提供兩組數值,並要用到聯立方程的方式解出兩個k值,再繼續後面的計算。我們會在講解題目時再作詳解。
歷年題目講解
HKDSE題目: Paper 1 Paper 2
HKCEE題目: Paper 1 Paper 2 (2003至2011年)
