做題目前請先對此課題有所熟悉。
部份題目用了k方法作解說,但考試時卷二無需列出步驟,所以可以不用設k去計算。
2025 Paper 2 Question 11
此題涉及三個數值的比例,所以先分拆做兩個比例,即第1個:第2個,同時第2個:第3個,以交叉相乘的方式計出y的值。我們發現到,左邊有8y,而右邊則有1個y,而答案並不需要計算y的值,所以可以把右邊全式乘以8,使兩式同樣是8y,便可以把兩邊的另一邊值做一個等於,從而計算及約簡得出答案。

2022 Paper 2 Question 12
題目只要求計算y:z的比較,所以在處理x:y=8:5時,可以利用主項轉換形式,把x成為全式的主項。
另一組公式,則把x化為含y的值,然後經運算後得出所需比例。
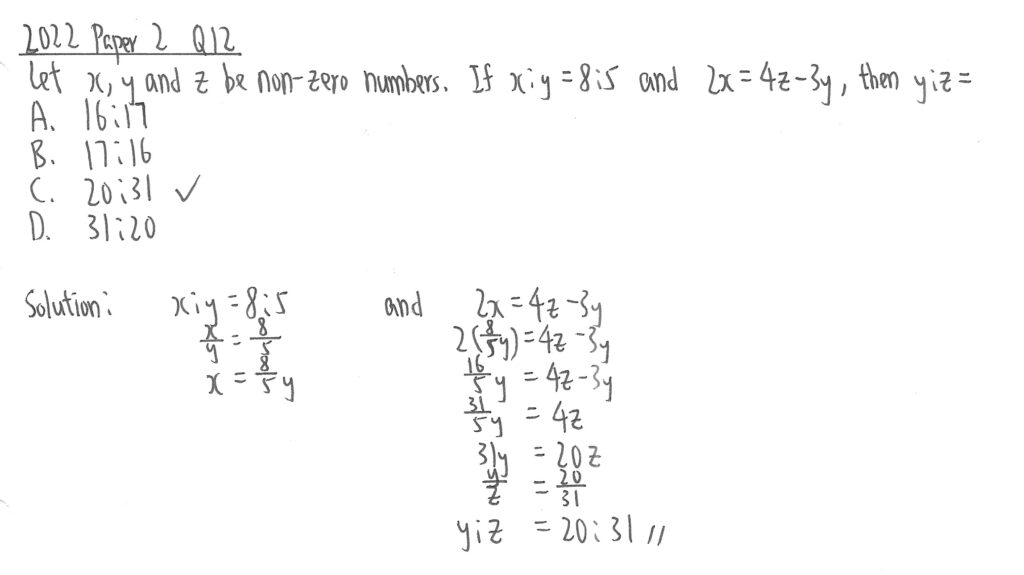
2021 Paper 2 Question 11
此題先用交叉相乘方式,計算出alpha和beta的值。由於經計算後只有1個alpha,所以所計算後半部時,直接把alpha化作16個beta,再經加減及約簡便可得出答案。

2019 Paper 2 Question 12
此題其實除了比例,還夾雜了「加權平均數」(Weighted average)的概念。即是說,分子是所用茶葉的總成本,而分母則是使用了多少公斤的茶葉,從而得出平均成本為$210。最後經運算及約簡得出x:y的比例。
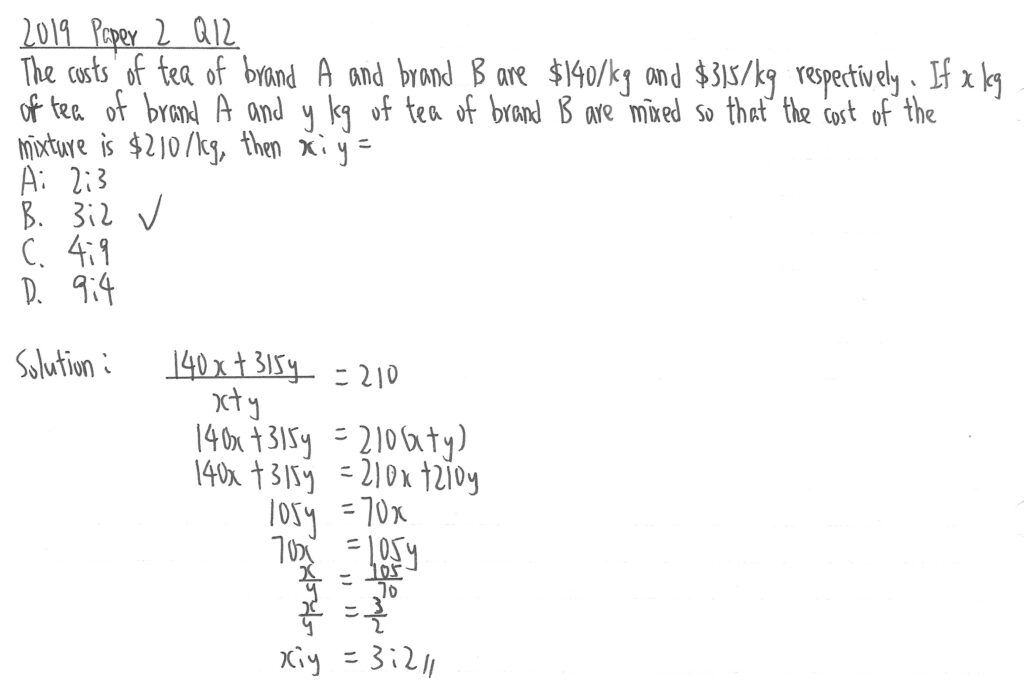
2018 Paper 2 Question 10
3a=4b可利用交叉相乘得出a:b的比例,與a:c的比例中的a值有不同。先計算出兩個a值的最小公倍數,然後把a:c的值各自乘2,得出兩個a的值同是4,便可以知道a:b:c的比例。再利用k方法,把題目最後的分數的a,b,c分別化為4k、3k及10k,經加減及約簡得出答案。

2016 Paper 2 Question 11
此題先用交叉相乘,經運算後可得出x:y比例值。

2015 Paper 2 Question 11
此題提供兩個比例,兩者雖然有c,但數值不同,所以要先找出最小公倍數6,然後a:c數值各自乘以2,同時b:c數值各自乘以3,使兩個比例的c值同是6,得出a:b:c,再分別設三個數是10k、9k及6k,計算後面比例的值。

2014 Paper 2 Question 12
此題可以先分拆為分數1:分數2,以及分數2:分數3,分別計出a:b,以及b:c的比例。之後發現到b值不同,所以要計算出兩個b值的最小公倍數1125,然後a:b值各自乘以45,同時b:c值各自乘以25,得出a:b:c後再比較那個值最大或最小。

2012 Paper 2 Question 9
此題可以利用交叉相乘以及同類項的加減,計算出x:y的值。

