餘式定理及因式定理題目,於卷二通常會獨立出題,並可能會夾雜其他課題一同考問。因此,除了餘式定理及因式定理要熟讀外,還需要熟讀其他課題,尤其是以下課題:
聯立方程 Simultaneous Equations
多項式除法公式:
被除式 (Dividend) = 除式 (Divisor) x 商式 (Quotient) + 餘式 (Remainder)
餘式定理 (Remainder Theorem):
當除式的最大次數是1,即x+a時,f(x)=-a (可以理解為x+a=0,所以x=-a)
因式定理 (Factor Theorem):
當利用餘式定理時,所計算出的餘式是0時,即該被除式可被除式整除(Divisible)
2025 Paper 2 Question 9
此題已知p(x)可被x+3整除,故先求出p(-3)=0時的n值,再把n值代入f(x)後,找出p(3)的值。
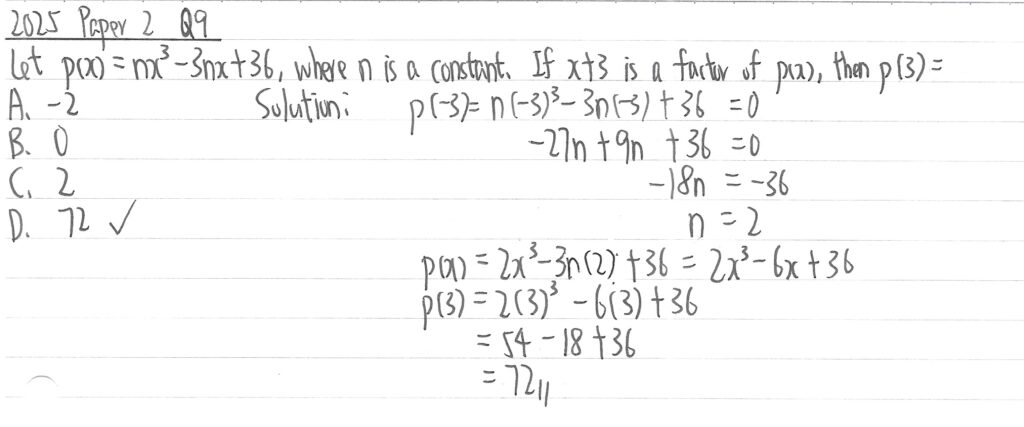
2024 Paper 2 Question 9
此題已知f(x)被x+k整除,所以先計算出f(-k)=0時的k值,再把n值代入f(x)。題目要求找出f(x)被x+1相除的餘式,所以應計算f(-1)的值。
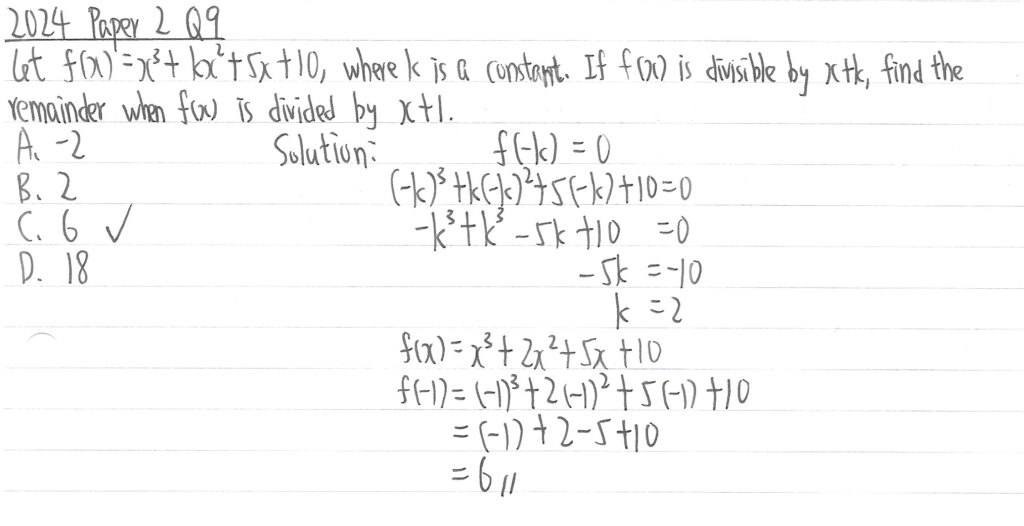
2023 Paper 2 Question 9
此題先計算當f(x)被2x-3整除後的a及b的主項值,即f(3/2)=0,然後計算被2x+3相除的餘式,即f(-3/2),把結果套落下面便可計算出其餘式值。

2022 Paper 2 Question 9
題目已知g(x)被x+2a整除,所以先計算當g(-2a)=0時的b值,再把結果套到f(x)後,按題目後面的求被x-2a相除的餘式時,求g(2a)時的餘式。
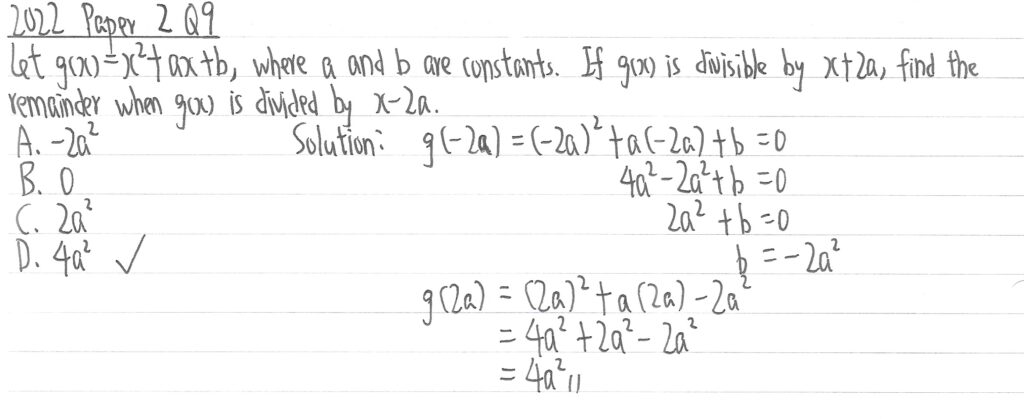
2021 Paper 2 Question 8
此題已知p(x)的除式(x2-1),所以先設商式為Q(x),而餘式是(ax+b),因為除式是2次方,所以餘式最多只會有1次方。已知p(x)被x+1相除時的餘式是-2,所以先設第一組式p(-1)=-2,同時也已知當p(x)能x-1整除,所以設第二組式p(1)=0,再利用聯立方程求出a及b值後得出餘式。兩式其實能夠使商式乘以0,所以商式在此並不重要。

2020 Paper 2 Question 6
已知x+2是g(x)的因式,所以先設g(-2)=0以求出a值,並把a值代入g(x)後計算出g(2)的值。

2019 Paper 2 Question 9
已知多項式能被2x+k整除,所以可以把所有x代入(-k/2)=0時的k值。

2018 Paper 2 Question 8
已知x-1是g(x)的因式,所以先設g(1)=0以求出b作為主項的值,並把b值代入g(x)後計算出g(-1)的餘式。
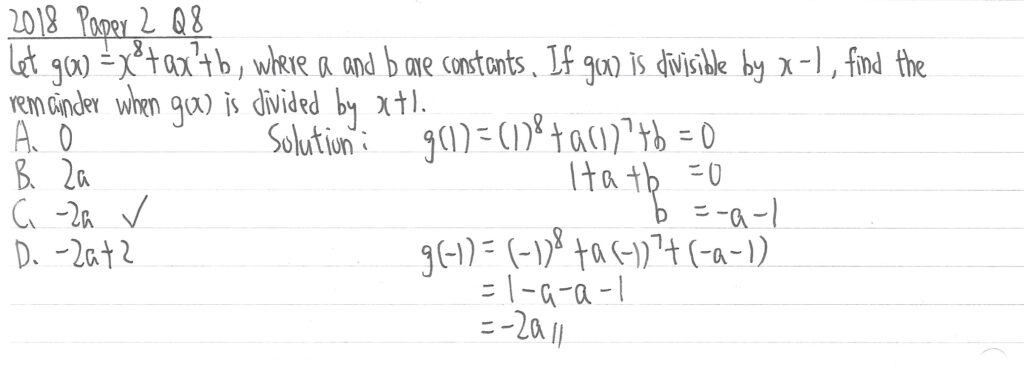
2017 Paper 2 Question 7
已知x-7是p(x)的因式,所以先設p(7)=0以求出c值,並把c值代入p(x)後計算出g(-1/2)的餘式。

2016 Paper 2 Question 6
已知2x+1是f(x)的因式,所以先設f(-1/2)=0以求出k值,並把k值代入f(x)後計算出f(-1)的餘式。

2013 Paper 2 Question 9
已知x+1是f(x)的因式,所以先設f(-1)=0以求出k值,並把k值代入f(x)後計算出f(1)的餘式。

2012 Paper 2 Question 4
已知多項式可被x+3整除,所以計算f(-3)=0下的k值。

