在閱讀以下題目分析前,請先熟讀此課題。
2011 Paper 1 Question 6
題目只要求計算在夏令營中的女生數目,所以當分別設x和y是男生和女生的數目後,可以先求x與y的比例為(1)式,再把其代入(2)式,便可把x抵銷,並計算y值,便是女生的數目。

2011 Paper 2 Question 6
當分別設x和y是每枝原子筆和每枝鉛筆的價錢後,發現兩式中x和y項的係數不同。在此情況下,可以先計出x和y在兩式係數中的最小公倍數,然後如下圖分析中,兩者以10x為目標,(1)式全式乘以2,同時(2)式全式乘以5,利用消除法互相抵銷10x,先計算y值,後代入其中一式計算x值。
題目要求計算購買3枝原子筆和2枝鉛筆的總價錢,所以可以設3x+2y,再把求出的x及y值代入並計算便可。

2010 Paper 1 Question 6
此題只要求計算一樽牛奶的價錢,當分別設x和y是一樽橙汁和一樽牛奶的價錢後,把(1)式的數值代入(2)式,使(2)式全部是y,便可直接計算出一樽牛奶的價錢。
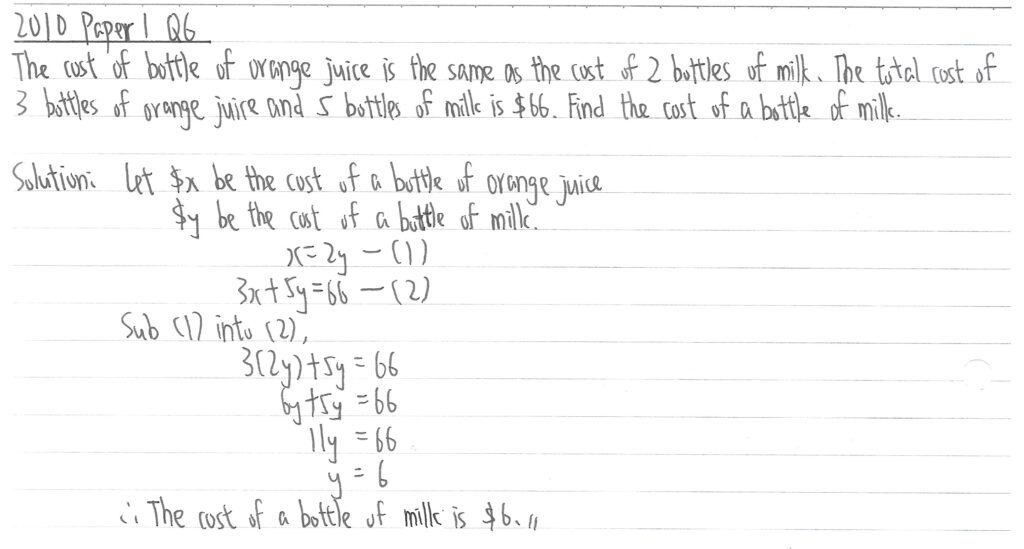
2010 Paper 2 Question 8
此題可以分拆為兩組右邊同是3的聯立方程。題目只要求計算q值,所以可以先把(2)式全式乘以2,使其變成2p,與(1)式一致並互相抵銷,便只剩下q並計算其值。

2009 Paper 1 Question 6
此題只要求計算John擁有的郵票數量,所以當分別設x和y是John和Mary分別擁有的郵票數量後,(1)式可以利用主項轉換方法,把y作為主項,並代入(2)式,使其變成只有x並直接求出John所擁有的郵票數目。

2008 Paper 2 Question 8
此題可以分拆出兩條聯立方程。不過,右邊發現兩邊n可以互相抵銷,所以可以先直接計算m值,再代入另一條公式便可計算n值。

2007 Paper 1 Question 7
此題只要求計算在某天,醫生看診了多少名長者病人。當分別設x和y是長者及非長者病人後,可以把(1)式作主項轉換,把y作為主項代入另一公式後,可直接計算x值,即長者病人的數目。

2007 Paper 2 Question 7
題目只要求計算一個蘋果的價錢。當分別設x和y是一個橙和一個蘋果的價錢後,先求出兩個x項中的係數的最小公倍數,所以(1)式全式乘以4,同時(2)式全式乘以3,使兩式同時是24x,利用消除法互相抵銷後只餘y,即蘋果的價錢並計算出來。

2004 Paper 1 Question 7
此題只要求計算購買橙的數量。在分別設x和y是所購買的橙和蘋果數量後,可以先把(1)式全式乘以3,使兩式同時出現3y,利用消除法互相抵銷後只剩下x,便可計算出購買的橙的數量。

2003 Paper 1 Question 6
此題要求計算在一程郵輪的總收入,即頭等客位票及經濟客位票的總和。題目已知兩種票的總和是600,而經濟客位票的銷售量是頭等客位票的3倍,所以計算時可利用代入法,先計算售出的頭等客位票數量,最後在計算總收入時,在計算經濟客位票數量時把數量乘以3便可。

2002 Paper 2 Question 8
此題可以直接分別代x和y是-2及1,再利用消除法計算a值便可。

1998 Paper 2 Question 4
此題可以把(2)式全式乘以2,使兩式同時出現2x,再利用消除法先計算y值,最後計算x值便可。

1997 Paper 2 Question 8
此題可以先把(1)式全式乘以2,使兩式同時出現2y,利用消除法先計算x值,再計算y值便可。

1995 Paper 2 Question 7
此題可以先把(2)式全式乘以2,使兩式同時出現4x,利用消除法先計算y值,再計算x值便可。

