此文會講解2003至2011年,香港中學會考(HKCEE)出現過有關變分(Variations)的題目。
2010 Paper 1 Question 10
此題是有關檯布的價格與其周界的關係。題目出現「Two parts」字眼,即是此題是部份變。價錢一部份與x正變,即在k方法下為k1x,另一部份則與x2正變,即k2x2。兩者相加便是檯布的總價格。
(a)部,分別代x=4及C=96,以及x=5及C=145,組成一組聯立方程,並求出兩個k值後代入公式便可。
(b)部,其實這是一個二次方程的問題,大家可以按計算機程式,得出兩個根,唯其中一個根是負值,在周界不可能是負值下,負值根便要捨去。

2007 Paper 1 Question 14
這是一題夾雜餘式定理(Reminder Theorem)及因式定理(Factor Theorem),以及變分的題目。
(a)部,已知f(x)能被x+3整除,所以第(i)部計算k值時,可以設x=-3代入f(x)中計算。
(a)(ii)部,則用多項式除法計出商式,商式再用二次方程方式做因式分解便可。
(b)部,題目出現「Two parts」字眼,即是此題是部份變的題目。前半與x3正變,利用k方法即是k1x3,後半與x2正變,即k2x2。兩者相加就是總價格(C)。
(i)部,分別代x=5.5及C=7381,以及x=6及C=9072,組成一組聯立方程,並求出兩個k值後代入公式便可。
(ii)部,先把972減到左式,再全式除以4後,會發現到左式其實就是(a)部的答案,所以可以套用(a)部答案=0,找出所有的根。由於長度不可能是負數,所以只有正數根才會是正確答案。

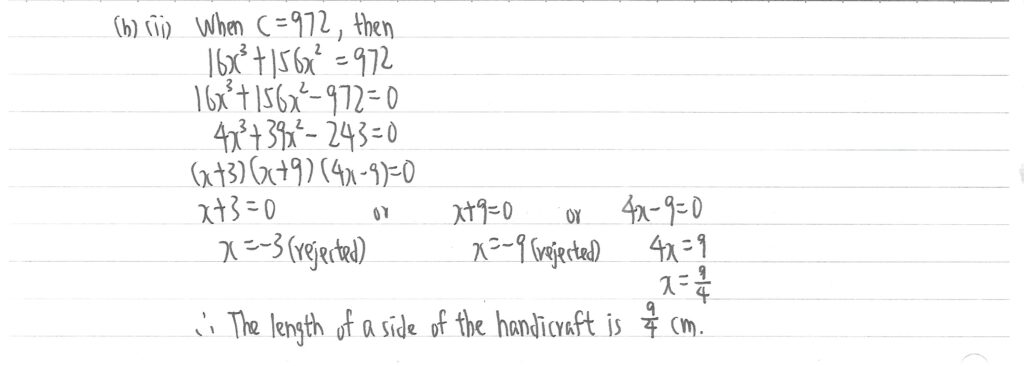
2005 Paper 1 Question 10
(a)部,題目出現「Two parts」字眼,即是部份變的題目。前半與x3正變,在k方法下即是k1x3。後半與x正變,即k2x。兩者相加成為f(x)的式。
再分別代f(2)=-6及f(3)=6,組成聯立方程求出兩個k值,代入f(x)式便可。
(b)部,f(x)直接代入(a)部答案得出g(x)公式。
(i)小題其實是餘式定理及因式定理題目,除式是x-3,即是如g(3)=0時,x-3就是g(x)的因式。
(ii)小題,利用多項式除法,計算出商值,並利用二次方程把商式再做因式分解便可。

2024 Paper 1 Question 10
題目出現「Two parts」字眼,即是部份變的題目。前半與x正變,在k方法下即是k1x。後半與x2正變,即是k2x2。兩者相加成為y的公式。
(a)部,分別代x=3, y=3,以及x=4, y=12,組成聯立方程並計算兩個k值,再把k值代入y的公式便可。
(b)部是二次方程當中的不等式,但如果以圖像方式表達,其實是一個開口向上的曲線,因為x2的係數是正數。另用判別式計算後,此二次方程會有兩個實根,即會穿過兩次x軸橫線,所以當y<0時,應該取中間部份的值域(Range)。

2003 Paper 1 Question 10
玩具太陽能車的速度與其行走距離有關。題目出現「Two parts」字眼,即是部份變的題目。前半與L正變,在k方法下即是k1L。後半與L2正變,即是k2L2。兩者相加成為V的公式。
(a)部,分別代L=10, V=30,以及L=15, V=75,組成聯立方程並計算兩個k值,再把k值代入V的公式便可。
(b)部是二次方程當中的不等式,但如果以圖像方式表達,其實是一個開口向上的曲線,因為x2的係數是正數。另用判別式計算後,此二次方程會有兩個實根,即會穿過兩次x軸橫線。當L大於或等於0時,應取兩根左右的範圍,因為兩邊的曲線均在正數位置。留意題目,最低的長度是5厘米,所以可能範圍要留意。

