此文章會講解,香港中學會考(HKCEE)於2003至2011年期間,有關變分(Variations)的卷二題目。
2011 Paper 2 Question 13
此為聯變的題目,a同時與b正變及與c2反變,在k方法下,b應放分子,c2應放分母,再代b=6,c=3,a=-2求出k值,最後根據k值,a=-9及c=4時計算b值。

2010 Paper 2 Question 16
此為聯變的題目,z同時與x及y2正變,在k方法下則兩者相乘,再用下圖方法計算便可。

2009 Paper 2 Question 14
題目出現Partly一字,即是此為部份變的題目。前半是常數,在k方法下則是k1,後者則與x反變,所以是k2/x,兩者相加得出y式。之後分別代x=1, y=-1,以及x=2, y=1,組成聯立方程求出兩個k值,再利用k值及代y=2計算最終的x值。

2008 Paper 2 Question 14
此為聯變的題目。y與x正變,所以在k方法下x放分子。同時y與z2反變,所以放分母。最後按下圖方法計算便可。

2008 Paper 2 Question 15
題目出現Partly一字,即是此為部份變的題目。前半與x正變,在k方法下即是k1x。後半與x2正變,即是k2x2,兩者相加便得出f(x)式。然後分別代f(1)=5及f(2)=16,組成聯立方程,求出兩個k值後代入f(x)中,最後計算f(3)的值。

2007 Paper 2 Question 14
題目出現Partly一字,即是此為部份變的題目。前半是常數,在k方法即是k1。後半與x正變,即是k2x,兩者相加得出y的公式。之後代x=2, y=17,以及x=4, y=11,組成聯立方程並計算兩個k值後代入y公式,最後代y=5求出最終的x值。
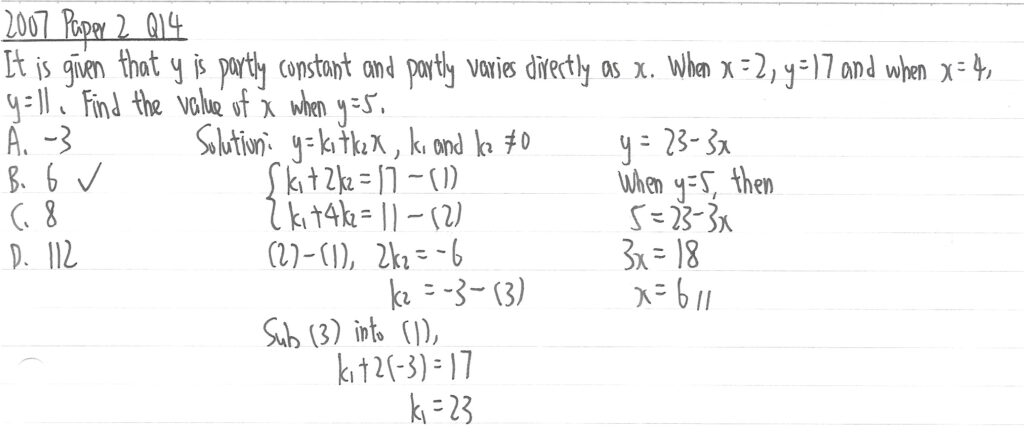
2006 Paper 2 Question 14
這是聯變的題目。x同時與y正變,在k方法下放分子,以及與z2反變,即是放分母。再利用下圖所示計算方法便可。

2005 Paper 2 Question 14
這是一題聯變的題目。z與y2正變,在k方法下放分子,同時與x反變,放分母。利用主項轉換方法把k作為主項便可求出答案。

2004 Paper 2 Question 16
題目有Partly一字,即是此伙為部份變題目。前半與x正變,即在k方法下是k1x,後半與x1/2正變,即k2x1/2,兩者相加便得出y公式。再代x=1, y=4,以及x=4, y=10,組成聯立方程求出k值後代入y式,再代x=16便求出y值。

2003 Paper 2 Question 14
這是一個聯變的題目。z與x2正變,在k方法下放分子,同時與y反變,在k方法下放分母。然後分別代x=4, y=3, z=2求出k值並代入y式,最後代入k值, x=2及z=3便可求出y值。

