變分(Variations)在HKDSE卷二中,由2012年至2025年,每年也會獨立出題。題目主要是聯變(Joint Variations),或是部份變(Partial Variations),而且可能夾雜其他課題一同考問。同學看以下題目講解時,請先閱讀此文熟悉課題。
2025 Paper 2 Question 12
這是一題聯變的題目,z同時與x3正變,以及與y2反變,前者應放分子,後者則應放分母,以k方法並分別代x=3、y=6及z=3,先找出k值,再用同一條式(知道k值後),再代x=5及y=2計出z值。

2024 Paper 2 Question 13
此為聯變的題目,因為z同時與x2正變及與y反變,所以在k方法下,x2應放分子,y應放分母,再按下圖進行計算。

2023 Paper 2 Question 13
這是一題聯變的題目,因為z同時與x2與y的立方根正變,在k方法下把兩數相乘,再代x=12,y=64,以及z=36先求k值,再代k值,x=16,y=729時,求出z的值便可。
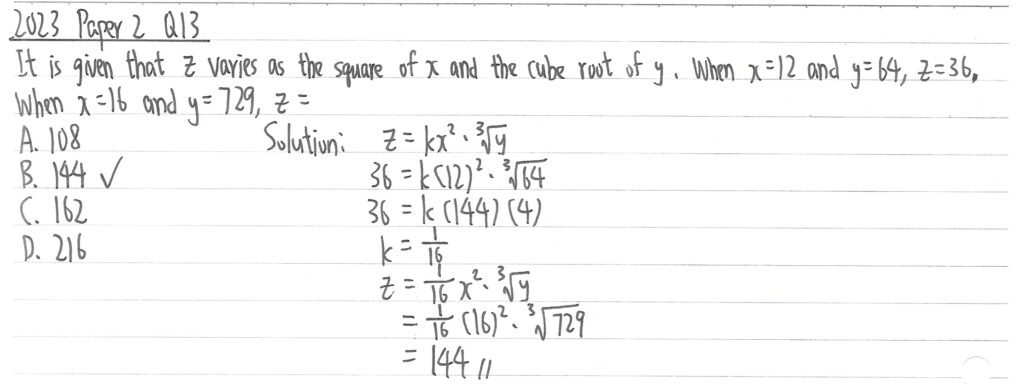
2022 Paper 2 Question 13
判斷題需要多做一些功夫才能判斷出句子的對錯。這是聯變的題目,以u作為主項。
(I)中,只要把全式倍大2次方便可。
(II)則先用主頂轉換把v作主項,再全式倍大2次方發覺是句子所說是錯的。
(iii)只需把w化作主項便可明顯看到與句子是相符。

2021 Paper 2 Question 12
此題是一個聯變的題目,因為w與x2正變,同時與y3反變,在k方法下前者放分子,後者放分母,再用主項轉換把k作為主項,再用分子分母互相調轉(即倒數)便可求出正確答案。

2020 Paper 2 Question 11
這是一題聯變的題目,因為w同時與u3及v的平方根正變,在k方法下可以相乘,再代u=2、v=4及w=8求出k值,再利用同一條式代k值、u=4及v=9下的w值便可。
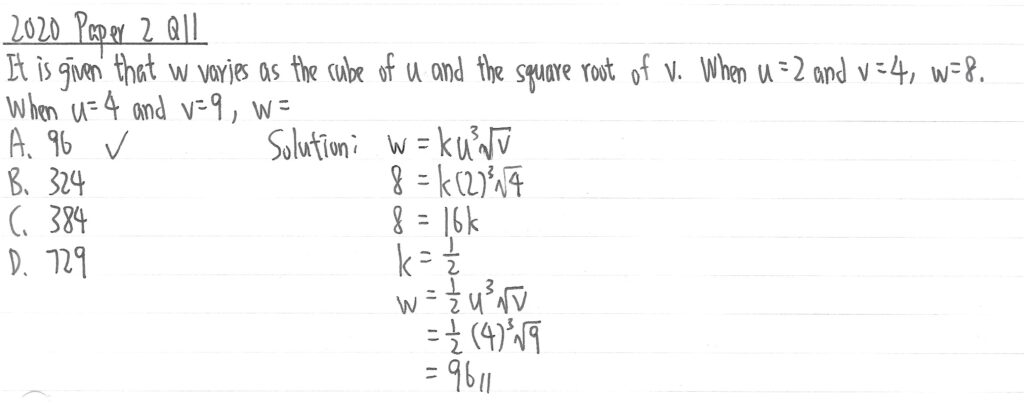
2019 Paper 2 Question 13
此為聯變的題目,因為z同時與x2正變及與y平方根反變,所以在k方法下,x2應放分子,y平方根應放分母,再按下圖進行計算。

2018 Paper 2 Question 11
此為一個聯變的題目,w同時與u的平方根正變,以及與v2反變,設公式後再用主項轉換把k作為主題,再全式乘大2次方便求出答案。

2017 Paper 2 Question 12
題目中有part字眼,所以是部份變的題目。前半是常數,所以在k方法下設k1,後半則與x2正變,所以設k2x2,兩者相加下得出y式。先分代x=1及y=7,以及x=2及y=13,組成一組聯立方程,先計出兩個k值後,再代x=3便可計出最終y值。

2016 Paper 2 Question 12
此為聯變的題目,因為z同時與x的平方根正變及與y反變,所以在k方法下,x的平方根應放分子,y應放分母,再按下圖進行計算。

2015 Paper 2 Question 12
此為一個聯變的題目,因為z同時與x3及y2正變,利用k方法相乘,並分別代x=2、y=1及z=14先計出k值,最後代k值,x=3及y=2計出最終的z值。

2014 Paper 2 Question 13
此為聯變的題目,z同時與x反變,以及與y3正變,在k方法下x放分母,y3放分子,再利用主項轉換把k作為主項,最後兩邊做倒數便求出正確答案。

2013 Paper 2 Question 13
此為聯變的題目,因為z同時與x的正變及與y平方根反變,所以在k方法下,x應放分子,y平方根應放分母,再按下圖進行計算。

2012 Paper 2 Question 10
題目出題Partly一字,所以是部份變的題目。前半與x2正變,在k方法下即k1x2,後半與x反變,所以是k2/x,兩者相加便得出y式。先代x=1及y=-4,以及x=2及y=5,組成聯立方程計出兩個k值,再利用k值代x=-2計出y值。

